Intégrammes (très difficile)

 

Dans ce post, nous parlerons d’intégrammes. En apportant des réponses aux questions naturelles qui se présenteront, nous (re)découvrirons des notions mathématiques parfois ardues mais plaisantes et… quelques problèmes encore non résolus.

Qu’est-ce qu’un intégramme ?

C’est une énigme logique. Voici un exemple :

Vive les vacances !

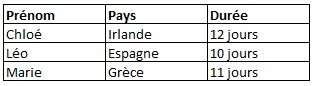
Ces trois amis, Chloé, Léo et Marie se racontent leurs vacances. Dans quels pays sont-ils allés et combien de temps ? Pour quel type d'hébergement ont-ils opté ?

Indices :

1. Chloé est partie plus longtemps que Léo.

2. Marie n'a pas fait de camping, n'a pas visité l'Espagne et s'est absentée moins longtemps que l'ami(e) qui a visité L'Irlande.

3. La personne qui est allée en Grèce y est restée plus de 10 jours, pas à l'hôtel.

4. On n'a pas campé en Irlande.

Univers des possibles :

Pays : Espagne, Grèce, Irlande

Durée : 10, 11 et 12 jours

Hébergement : chez un ami, en camping, à l’hôtel

Avez-vous trouvé la réponse ? La voici :

Vous êtes en droit de vous poser les questions suivantes :

• Est-ce qu’il n’y a qu’une seule réponse à cette énigme ?
  
• Les indices qui sont fournis sont-ils tous utiles ?
• Combien y a-t-il de solutions envisageables ?

La réponse est positive aux deux premières questions et vous pourrez vous en convaincre facilement par vous-même. Mais nous verrons qu’elles soulèvent, dans des cas plus généraux, des problèmes complexes.

Quant au nombre de solutions : Il faut attribuer à chaque prénom un pays, une durée, un hébergement. Les valeurs de chacun de ces champs peuvent adopter 3! positions. Il y a donc 3!³ = 216 solutions envisageables

Généralisons maintenant la notion d’intégramme :

Un intégramme est une énigme logique constituée

• d'un titre,
• d’un texte introductif qui situe le contexte (on l’appelle « chapô »),
• d’un ensemble de champs qui peuvent prendre un certain nombre de valeurs distinctes (le même nombre pour chaque champ),
• d’un ensemble d’indices qui permettent d’associer les valeurs entre elles.

Des revues existent qui proposent de tels intégrammes. Elles sont généralement caractérisées par un niveau de difficulté (croissant au sein de la revue). Chaque intégramme comporte une solution unique et, si la revue est de bonne qualité, il n’y a pas d’indices inutiles.

Grille de résolution

Pour faciliter la résolution d’un intégramme, une grille telle que celle-ci est utile :

A quoi sert cette grille ?

Il faut voir la solution comme le pallier en haut d’un escalier, et les cases de cette grille comme les marches qui permettent d’y parvenir. Le joueur peut compléter chaque case par un O (Oui) ou un N (Non), au fur et à mesure de son avancée dans les déductions.

Ainsi, puisque l’indice 4 nous dit qu’on n’a pas campé en Irlande, on peut compléter la case C5 par un N. C’est une déduction très facile.

Chaque ligne et chaque colonne d’un groupe de cases, ne peut contenir qu’un seul O.

La grille a globalement une forme triangulaire. La partie en bas à droite est vide de cases car elles correspondraient à des cas qui sont déjà décrits dans la partie supérieure gauche.

Parfois, certains intégrammes ne comportent aucun indice et ne sont constitués que d’une grille qu’il faut remplir entièrement. On les appelle des intégrammes muets.

Certains intégrammes sont plus difficiles que d’autres. Pourquoi ?

La taille de l’intégramme est un facteur important car elle augmente le nombre de solutions envisageables. Ainsi, un intégramme à 4 champs de 5 valeurs a (5!)^(4-1) = 1 728 000 solutions. C’est le format le plus courant que l’on trouve dans les revues.

Mais la taille ne fait pas tout. La résolution est une succession de déductions élémentaires et la difficulté globale est essentiellement celle de la déduction la plus difficile. C’est le cas aussi quand on grimpe un rocher à Fontainebleau… Tant que la fatigue ne rentre pas en jeu, c’est le passage le plus ardu qui crée la difficulté globale, un peu comme une chaîne qui a la solidité de son maillon le plus faible.

C’est tout l’intérêt de la grille présentée plus haut que de procurer des étapes simples dans le processus de déduction.

Chaque déduction intermédiaire (c'est-à-dire le fait de remplir une case de la grille avec un O ou un N) met en jeu un certain nombre d’indices ou de déductions antérieures (qui peuvent être alors vues comme de nouveaux indices). Ce nombre est un élément majeur de la difficulté d’une étape.

Qu’est-ce qu’une déduction difficile ?

Une déduction peut faire appel à plusieurs indices, ou plusieurs indices et plusieurs cases de la grille (que l’on peut voir alors comme de nouveaux indices). Plus il y a d’indices/cases considérés, plus la déduction est difficile à comprendre.

L’expérience indique qu’au-delà de 3 indices permettant une déduction, celle-ci est difficilement accessible à un esprit humain. Elle doit alors être décomposée, si possible, en une série de sous-déductions. Parfois cela n’est pas possible et on a affaire à un intégramme très difficile.

Les lignes qui suivent donnent un exemple de déductions très difficiles. Le lecteur qui le souhaite peut directement passer à la suite.

Quatre amis professeurs de français se sont retrouvés pour corriger l'écrit du bac blanc de leurs élèves. Combien de copies ont-ils notées ? Quelles sont les meilleure et pire notes qu'ils ont attribuées ? Depuis combien de temps enseignent-ils ?

Univers proposé :

Prof. Marc, Mélissa, Oriane, Pascal

Copies 24, 25, 26, 27

Meilleure 15/20, 16/20, 17/20, 18/20

Pire 6/20, 7/20, 8/20, 9/20

Durée 10 ans, 12 ans, 14 ans, 16 ans

Indices :

1. Mélissa, qui n'a pas noté 24 copies, a mis un point de plus au meilleur devoir que la personne qui en a corrigé 27. Sa pire note est de deux points au-dessus de celle de l'enseignant(e) qui a 16 ans d'ancienneté.

2. L'enseignant(e) au 17/20 exerce depuis deux ans de plus que Marc.

3. Le/la professeur(e) au 18/20 a noté deux copies de plus que celui/celle qui enseigne depuis 10 ans.

4. La meilleure note de la personne dont la pire était un 6/20 a un point de moins que celle de Pascal, qui n'a pas commencé il y a 12 ans.

5. Oriane enseigne depuis quatre ans de plus que l'enseignant(e) au 9/20 et a noté une copie de moins que celui/celle qui a donné un 8/20.

Les déductions

J1 = Non (Marc n’a pas mis 7/20 comme pire note),

F6 = Non (le/la prof aux 12 ans d’ancienneté n’a pas mis un 16/20 comme meilleure note)

... ne peuvent pas être obtenues au travers d’étapes intermédiaires obtenues sur la grille.

Elles nécessitent la considération de trois indices pour être obtenues : l’indice 1, le 4 et le 5.

Ce sont des déductions extrêmement difficiles qui nécessitent des raisonnements complexes. Je laisse aux lecteurs courageux le soin de les mener.

Avant d’aller plus loin, voyons quelques exemples de déductions faciles : les déductions de grille, déduction qui peuvent être menées en ne considérant que la grille de résolution.

Le complétement

C’est le cas le plus élémentaire qui consiste à compléter un groupe de cases qui comporte un O : les cases qui sont sur la même ligne et la même colonne de ce groupe de cases peuvent être complétées par des N puisqu’une ligne ou une colonne, au sein d’un groupe de cases, ne comporte toujours qu’un seul O.

Inversement, une ligne (ou une colonne) d’un groupe de cases qui est constitué de N, sauf une case, engendre le remplissage de la case vide par un O.

La correspondance (ou pivot)

Il s’agit d’un autre cas de déductions de grille. Nous allons l’étudier sur l’exemple précédent.

Imaginons que nous soyons à ce stade de résolution :

Nous savons qu’on a fait du camping en Espagne (A5 = O) et que le camping n’a pas duré 12 jours (F5 = N). Nous pouvons alors déduire que la case A9 = N : En Espagne, on n’est pas resté 12 jours.

Il s’agit d’une « correspondance », encore appelée « pivot » car le N de F5 semble se transposer en A9 en pivotant autour de A5.

L’incompatibilité

Imaginons cette fois que nous soyons à ce stade de de la résolution :

On note que Léo n’est pas allé en Grèce ni en Irlande. Par ailleurs, l’hôtel n’a pas été utilisé en Espagne.

Les valeurs « Léo » et « Hôtel » ne sont donc pas compatibles. Car si elles étaient associées, il ne resterait aucun pays disponible. On peut donc déduire que I2 = N

On parle de déduction par incompatibilité.

La croix de non

Pour illustrer ce type de déduction, qui est une autre déduction de grille, il nous faut une grille avec plus de valeurs par champ. En voici une :

On constate que Clémence et Hugo ne sont pas archiviste, ni postier, ni serveur. L’un est donc animateur et l’autre vendeur. En conséquence, Charlie, Louise et Marine ne sont pas animateur ni vendeur.

On peut alors déduire que les cases D1, E1, D4, E4, D5 et E5 valent N.

L’aspect obtenu, dans cette configuration justifie l’appellation de « croix de non » (l’ensemble des N a plus ou moins la forme d'une croix).

Ces déductions de grille (complètement, pivot, double croix de non) sont relativement faciles. Il faut juste être attentif pour les déceler.

L’hypothèse

Les déductions de grille issues d’hypothèses sont en revanche nettement plus difficiles.

Ce type de déduction consiste à supposer qu’une case prend une certaine valeur et, par une suite de déductions, à aboutir à une contradiction. Plus la suite de déductions est longue, plus l’hypothèse est difficile.

Pour les lecteurs qui veulent se faire une idée, un exemple est développé dans les lignes qui suivent. Les autres pourront passer directement à la suite.

Considérons la grille suivante :

Cette grille est introduite de la manière suivante :

Ce soir, chacune de ces personnes suivra un film sur Internet. Quelle est la durée du téléchargement ? Quel genre de film a-t-elle choisi ? Combien de jours dure la location et combien de fois peuvent-elles le visionner ?

Elle ne permet à ce stade aucune des déductions de type « incompatibilité, « correspondance » ou « Croix de non ».

On pose alors une hypothèse : on suppose que A1 = O. Nous aboutirons à une contradiction.

Si A1 = O alors, par déductions de grille simples (de type trois Non => un Oui, ou un oui => trois Non), on peut remplir le groupe de cases en haut à gauche (on commence par A2 = O car A1 = O, puis B2 = O car B2 = C2 = D2 = N, etc.)

Viennent ensuite toute une série de déductions par correspondance autour des pivots A1, B2, C3 et C4.

Je donne la 1^re : A1= Oui (pivot) et P1 = Oui donc A8 = Oui

Les autres sont indiquées en vert.

On complète alors les trois blocs de cases de gauche par des déductions simples, notées en bleu.

A ce stade, grâce à ces blocs de gauche, on sait tout sur tout le monde. Reste à trouver une éventuelle contradiction avec les autres blocs. C’est le cas : G11 nous dit que les 21 jours ne sont pas associés à l’horreur. Mais D11 et D15 nous disent le contraire.

L’hypothèse est donc rejetée => A1 = N

Lien entre la résolution d'un intégramme et certaines théories mathématiques

Il existe des liens étroits entre les intégrammes et :

• la théorie des impliquants premiers (prime implicants),

• la dualité entre les formes conjonctives normales et les formes disjonctives normales,

• le problème des couvertures d'ensembles (set cover) ou son équivalent dual, le problème du hitting set.

Voyons les choses une par une, sans nous laisser impressionner…

Lien avec la théorie des impliquants premiers

Nous allons introduire le 1er lien au travers du tout 1er exemple simplifié : on n’y parlera pas d’hébergement.

Titre : Vive les vacances !

Chapô : Ces trois amis se racontent leurs vacances. Dans quels pays sont-ils allés et combien de temps ?

Indices :

1. Chloé est partie plus longtemps que Léo.

2. Marie n'a pas visité l'Espagne.

3. Marie s'est absentée moins longtemps que l'ami(e) qui a visité l'Irlande.

4. La personne qui est allée en Grèce y est restée plus de 10 jours.

Le nombre de possibilités est de (3!)^(3-1) = 36. C’est peu pour jouer mais assez pour raisonner sur les impliquants premiers.

Voici la solution :

 Et la grille de résolution

Représentons maintenant l’univers des possibilités dans un tableau. Ce tableau a autant de lignes que de solutions envisageables dans l’intégramme : 36.

La ligne d’en-têtes est construite ainsi :

PC, PL et PM désignent les pays respectivement visités par Chloé, Léo et Marie.

De même, DC, DL et DM désignent les durées respectives.

I1 désigne le 1er indice. La valeur de la ligne correspond à 1 s’il est vérifié, 0 sinon.

Ainsi, dans la 1^re ligne, I1 vaut 0 car Chloé est partie 10 jours, donc moins longtemps que Léo, ce qui est incompatible avec I1.

De même I2, ... I4 font référence aux autres indices.

Enfin, A1, B1, … C6 font référence aux cases de la grille de résolution et valent 1 si la case est remplie d’un O (oui), d’un 0 sinon.

Ainsi A1 = 1 pour la 1^re ligne car Chloé est bien partie en Espagne dans cette situation.

Il n’existe qu’une ligne (la 8e à partir de la fin) où I1 = I2 = I3 = I4 = 1. Elle correspond à la solution de l’intégramme : Chloé a séjourné en Irlande 12 jours, Léo en Espagne 10 jours, Marie en Grèce 11 jours.

Notons que « trouver la solution dans ce tableau » n’est pas du tout la même chose que « trouver une méthode de déduction convaincante ». Nous allons nous y atteler. Mais avant, regardons les précisions et utilités des indices :

Précision et utilité d'un indice

La précision d’un indice est le nombre de solutions possibles qui sont compatibles avec lui. Dans l’exemple précédent, la précision de l’indice 1 est 18.

L’utilité d’un indice est le nombre de solutions qui sont compatibles avec tous les autres indices. Dans l’exemple précédent, l’utilité de l’indice 1 est 2. En effet, il existe seulement deux lignes où I2 = I3 = I4 = 1.

Si l’utilité est 1, l’indice est inutile puisque, sans lui, on a toujours une solution unique. Un intégramme de qualité ne doit pas en contenir : tout indice doit être indispensable et donc avoir une utilité strictement supérieure à 1.

Plus l’utilité est élevée, plus l’indice « contrôle » les solutions. Il est recommandé, lors de la création d’un intégramme de répartir les utilités assez uniformément. Mais on peut déroger à cette règle.

Observons les précisions et utilités de tous les indices. On constate que c’est le 3e indice qui est le plus précis et qui apporte le plus d’information. Sans lui, il reste 8 possibilités.

 Sur le diagramme qui suit, on observe l’influence de chaque indice sur les 36 solutions.

Ainsi, il y a 7 solutions qui compatibles avec I1, I2 et I4 mais pas avec I3

et 7 autres compatibles avec I2 et I4 mais pas avec I1 ni I3

Au centre du diagramme, on trouve la seule solution compatible avec tous les indices.

A noter, également, qu’une solution (en haut à gauche), n’est compatible avec aucun indice.

Voyons maintenant les implications.

Implication et impliquant premier

On dit qu’un indice implique une case donnée quand la connaissance de cet indice, permet d’attribuer une valeur (O ou N) à la case.

Concrètement, dans notre grand tableau qui précède, chaque fois qu’un indice indique 1, la case, pour être impliquée, doit indiquer toujours 1 (elle vaudra alors O = 1 = Oui) ou toujours 0 (elle vaudra alors N = Non = 0).

On s’attend notamment que l’indice 2 (Marie n'a pas visité l'Espagne) implique A3 (qui vaut N). C’est bien le cas : partout ou I2 = 1, on a A3 = 0 (et, ce qui revient au même, partout où A3 = 1, on a I2 = 0)

Si on recherche de manière systématique, ce qu’on peut faire avec un programme informatique simple, voici toutes les implications qu’on obtient :

Ainsi, l’indice 1 (Chloé est partie plus longtemps que Léo) permet de déduire que Chloé n’est pas partie 10 jours (D1=N) et que Léo n’est pas parti 12 jours (F2=N).

De même, l’indice 3 (Marie s'est absentée moins longtemps que l'ami(e) qui a visité l'Irlande) permet de déduire que Marie n’est pas partie en Irlande (C3=N), que Marie n’est pas partie 12 jours (F3=N) et que la personne qui a visité l’Irlande ne s’est pas absentée 10 jours (C4=N).

Il n’existe évidemment pas de combinaisons d’indices plus efficace pour déduire les 7 cases précédentes puisqu'elles sont issues d'un seul indice.

On dit que I1 est un impliquant premier de D1 et F2. De même I2 est un impliquant premier de A3, etc.

Plus généralement, on dit qu’un indice, ou une combinaison d’indices, est un impliquant premier d’une case si

• cette combinaison permet de déduire (implique) la case,

• toute sous-combinaison de ces indices ne permet pas la déduction.

Le nombre d’indices contenu dans une telle combinaison d’impliquants premiers est l’ordre de l’impliquant.

Un impliquant premier correspond au principe du rasoir d’Ockham qui indique que les explications les plus simples doivent être privilégiées.

C’est un puissant outil pour mettre au point des déductions, étant donné une solution à atteindre. En particulier, il est utilisé dans l’industrie, dans le diagnostiquer les causes probables des pannes.

Nous venons de découvrir que l’indice 2 est un impliquant premier d’ordre 1 de la case A3.

Mais qu’en est-il des autres cases ? Il faut plusieurs indices pour les déduire. D’ailleurs, maintenant que nous avons formellement déduit 7 cases, nous pourrions les considérer comme de nouveaux indices… Mais nous ne le ferons pas pour le moment.

Essayons toutes les combinaisons d’ordre 2 et voyons quelles cases sont impliquées.

I1 et I2 permettent de déduire D1, F2, A3 (mais nous le savions déjà) et rien d’autre.

(I1, I2) n’est donc l’impliquant premier d’aucune case. Nous ne les noterons pas dans le tableau qui suit qui récapitule les nouvelles cases déduites avec seulement 2 indices. Il y en a 9.

Essayons de comprendre pourquoi, de I2 et I3, on déduit que la case B3 vaut O. Pour cela, redonnons du sens à ces sigles :

I2 : Marie n'a pas visité l'Espagne

I3 : Marie s'est absentée moins longtemps que l'ami(e) qui a visité l'Irlande.

B3 = O : Marie est allée en Grèce.

C’est logique : de I2, on déduit que Marie n’est pas allée en Espagne, de I3 qu’elle n’est pas allée en Irlande. Elle est donc allée en Grèce !

A ce stade, nous avons déduit, avec un seul indice, 7 cases, et avec 2 indices, 9, soit 16 en tout.

Gardons bien à l’esprit que, dans un raisonnement plus classique, nous aurions dû, après la déduction des 7 premières cases, considérer ces 7 cases comme de nouveaux indices.

En vert les cases dont l’impliquant premier est d’ordre 1, en rose celles d’ordre 2.

On note que certaines cases de couleur rose auraient pu être facilement déduites à partir de déductions de grille. C’est le cas de B3 = O.

C’est d’ailleurs tout l’intérêt des cases de la grille que d’offrir des étapes simples.

Si l’on fait le travail en totalité, voici la cartographie obtenue :

Ainsi, si l’on refuse d'emprunter les « marches intermédiaires » que sont les cases de la grille en tant que déductions intermédiaires, et si l’on n’utilise toujours que les indices, les cases en rouge demanderont alors toujours la mise en œuvre des 4 indices tandis que celles en vert, n’en demandent qu’un seul.

Ce tableau nous dit (case C6) que l’on peut déduire des indices 1 et le 3 le fait que Chloé est partie 12 jours. Saurez-vous le faire ?

Et des indices 3 et 4, saurez-vous déduire qu’on est parti en Espagne 10 jours ?

Proposition de démarche déductive

Résoudre un intégramme, ce n’est pas seulement, bien entendu, considérer les indices. Il faut s’appuyer sur les cases de la grille pour déployer un raisonnement le plus simple possible à chaque étape. Nous avons pour le moment négligé cette étape pour étudier tout ce que l’on pouvait faire directement avec les indices. Mais déduire quelque chose avec 3 indices ou plus est très compliqué.

Généralement, la démarche adoptée pour bâtir une démonstration est la suivante :

1. Pour chaque indice I1, …, In, déterminer l’ensemble des cases impliquées par cet indice.

2. Faire ensuite toutes les déductions de grilles possibles et obtenir de nouvelles cases déduites

3. Retirer, de l’ensemble des cases impliquées/déduites à l’étape précédente, les cases N qui sont liées directement à une case O dans la même ligne ou la même colonne du groupe de cases (savoir que Marie n’est pas allée en Espagne n’apporte rien si l’on sait qu’elle est allée en Grèce)

4. Déterminer, parmi la liste des indices les indices, ceux qui sont impliqués par l’ensemble de toutes les cases déduites (ils sont devenus inutiles car toute leur information est désormais présente dans la liste des cases déduites)

5. Considérer comme nouvelle liste d’indices : les indices I1, … In, desquels on ôte les indices impliqués et auxquels on ajoute les cases déduites. Cette nouvelle liste regroupe toute l’information à exploiter.

6. Pour chaque couple d’indices, déterminer l’ensemble des cases impliquées par ce couple d’indices.

7. Refaire les étapes 2., 3., 4., 5. et 6.

8. Recommencer avec des triplets d’indices.

On ne poursuit généralement pas avec des quadruplets car les déductions sont alors le plus souvent inaccessibles à l’esprit humain.

Si le processus de déduction n’est pas terminé avec les triplets, on tente une hypothèse et on reprend ensuite au début.

Si l’on applique cette démarche à l’exemple précédent, seules les deux premières étapes sont mises en œuvre car l’intégramme est très simple.

Etape 1. : On prend les indices un par un et on obtient 7 cases déduites :

Etape 2. : On fait des déductions de grille. On obtient toutes les cases ! Nous laissons au lecteur le soin de le faire

Forme conjonctive normale (FNC) et forme disjonctive normale (FND)

Pour introduire et illustrer cette partie, intéressons-nous spécifiquement à la case E1 dans le grand tableau de 36 lignes précédent.

Dans la solution de l’intégramme, E1 = 0 (Non) : Chloé n’est pas partie 11 jours.

Considérons uniquement les colonnes composées des 4 indices et de E1. Et éliminons au passage les lignes similaires. On obtient le tableau ci-dessous :

Séparons maintenant le tableau en deux sous-tableaux A et B :

Le tableau B, répertorie toutes les situations où la case E1 = 1 = Oui (qui n’est pas la solution). Ainsi, la 1^re ligne indique que les indices I3 et I4, pourtant vrais dans ce cas, ne suffisent pas pour impliquer E1 = N.

Il faut donc impérativement I1 ou i2 pour avoir implication de E1. De même, il faut I1 ou I3 (2^e ligne), I1 ou I4 (3e ligne), etc.

On exprime la condition nécessaire générale ainsi :

E_Impl = (I1 ou I2) et (I1 ou I3) et (I1 ou I4) et (I2 ou I3 ou I4) et (I2 ou I3) et (I3 ou I4) et I3

Ou, en notation plus condensée (on note « ou » par une somme et « et » par un produit) :

E_Impl = (I1+I2) (I1+I3) (I1+I4) (I2+I3+I4) (I2+I3) (I3+I4) I3

Pour ceux qui sont intéressés, voici quelques rappels d’arithmétique booléenne :

Les « et » devenant des produits et les « ou » devenant des sommes permettent de faire des calculs. Il faut simplement accepter que 1 + 1 = 1 et non 2...

Et plus généralement que

a + a = a (la porte est ouverte ou la porte est ouverte = la porte est ouverte)

a (a + b) = a (la porte est ouverte et (la porte est ouverte ou le chien aboie) = la porte est ouverte)

a a = a (la porte est ouverte et la porte est ouverte = la porte est ouverte)

On parle alors de forme normale conjonctive (FNC) car c’est un produit (et) de sommes (ou).

Pour avoir implication de E1, il faut impérativement que les indices satisfassent cette forme normale conjonctive.

Réciproquement, si on a cette forme, alors on n’est pas dans le tableau B, et donc on est nécessairement dans le tableau A, où E1 est bien vérifiée.

Cette forme conjonctive est donc la condition nécessaire et suffisante pour que E1 soit impliquée.

Il existe un résultat mathématique qui indique qu’on peut toujours transformer une forme normale conjonctive en une forme normale « minimale » (au sens taille minimale). En l’occurrence, en utilisant le fait que, pour tout a et pour tout b, a (a+b) = a, on constate que (I1+I2) (I1+I3) (I2+I3+I4) (I2+I3) (I3+I4) I3 = (I1+I2) I3, et on obtient la forme normale minimale:

E1_Impl= i3 (i1+i2) (i1+i4)

Pour déduire E1, il faut donc

I3

ET

I1 ou I2

ET

I1 ou I4.

I3 apparaîtra donc toujours dans les impliquants premiers de E1. C’est bien le cas : impossible de déduire E1 sans utiliser l’indice 3.

Il existe aussi un résultat qui indique que, toute FNC peut être écrite sous forme de FND, forme normale disjonctive (somme de produits) qui, elle aussi, bénéficie d’une formulation minimum

En l’occurrence, elle vaut : E1_Impl= i1 i3 + i2 i3 i4

En effet si l’on utilise que pour tout a et tout b, a a = a et que ab + a = a (logique booléenne)

E1_Impl

= i3 (i1+i2) (i1+i4)

= (i1 i3 + i2 i3) (i1+i4)

= i1 i1 i3 + i1 i3 i4 + i1 i2 i3 + i2 i3 i4

= i1 i3 + i2 i3 i4

Ceci indique que, pour déduire E1, il faut

I1 et I4

ou

I2 et I3 et I4

Notons que, hélas, le passage CNF => DNF minimal est un problème NP-complet, dont la solution est facile à vérifier mais dont la résolution est difficile.

Ce n’est donc toujours pas simple de résoudre un intégramme… Mais nous le savions.

Toutefois, à condition d’utiliser certains algorithmes performants, on parvient à faire cette transformation dans la majorité des cas. Ceci est une méthode pour déduire des impliquants premiers à partir d’un ensemble d’indices et du tableau des possibilités, et donc de bâtir une démarche déductive.

Car les impliquants premiers sont les briques de base d’une démonstration !

Problème de la couverture d’ensemble

Reprenons le tableau B précédent concernant E1

On a vu qu’il fallait nécessairement I1 ou I2 (1^re ligne), I1 ou I3 (2^e ligne), etc., pour déduire E1.

Choisir un indice, c’est en fait choisir une colonne du tableau.

Dire que I1 ou I2 sont nécessaires pour satisfaire la condition imposée par la 1^re ligne, c’est dire que la colonne I1 ou la colonne I2 doit intersecter l’un des deux 0 de la ligne 1.

Finalement, il faut avec un minimum de colonnes, atteindre toutes les lignes au niveau des 0.

Il se trouve que

• I1 + I3 est une solution qui fonctionne pour toutes les lignes : ces deux colonnes intersectent au moins un zéro sur chacune des lignes

• I2, I3, I4 en est une autre

Ce sont d’ailleurs les seules et on retrouve bien les impliquants premiers précédents.

Cette notion d’atteinte d’un élément (un 0) au sein d’un jeu d’ensembles (les lignes) est exactement le problème du « hitting set », qui est, une fois de plus, un problème NP-complet, et même l’un des 21 problèmes NP-complets de Karp.

En conclusion, qu’avons-nous appris ?

Nous avons appris qu’une petite énigme amène à un univers de questions intéressantes.

Démontrer, prouver, c’est trouver un chemin simple dans un dédale de déductions possibles.

Cela peut se faire par la construction d’un tableau de possibilités et par l’extension, à petits pas, de l’univers connu, jusqu’à ce que sa frontière atteigne la solution.

Livingstone n’a pas fait autrement pour trouver les sources du Nil !

Cette exploration nous a conduit jusqu’aux impliquants premiers, aux formules normales booléennes, et à la notion de couverture d’ensembles.

Je vous laisse méditer là-dessus...

Références

[1] https://fr.wikipedia.org/wiki/Int%C3%A9gramme

Remarque : dans l'article Wikipédia (plutôt décevant), on parle du "très difficile intégramme d'Einstein". Mais il n'est pas difficile et encore moins d'Einstein...

[2] https://fr.wikipedia.org/wiki/Probl%C3%A8me_NP-complet

[3] https://en.wikipedia.org/wiki/Implicant

[4] https://fr.wikipedia.org/wiki/Forme_normale_conjonctive

[5] https://fr.wikipedia.org/wiki/Forme_normale_disjonctive